Tripping Over Words
As a parent of two children making their way through math education, I have the privilege to talk with them about learning on a regular basis. Sometimes it's at the dinner table when I throw them a neat question to think about and sometimes it's in the car driving to hockey/baseball/guides/whatever. Talking about education with my kids is one of my favourite things to do and they really seem to enjoy it too.
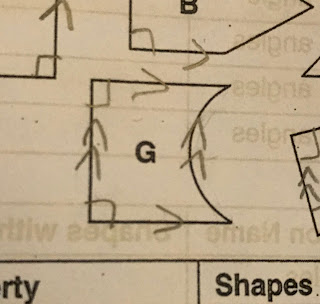
The other evening, my daughter Megan took out a worksheet that she had been working on in her grade 6 class. The students' task was to identify lines in 2-D shapes that were either parallel or perpendicular and they were to sort these shapes based on their geometric properties. I'd imagine this type of activity is fairly common in Ontario as these sorts of comparing and sorting activities are written as part of our grades 1-8 mathematics curriculum. While talking to Megan about her school work, I noticed her notation on figure G indicating that the lines were parallel:
I asked Megan about figure G and she said that the two "vertical" lines were parallel because they were two lines that will never touch. She explained that the straight line would continue running straight up & down and the curved "line" would continue in a circle, they'd never touch and were therefore parallel. I thought this was somewhat odd as the term parallel is first introduced in grade 3 in Ontario, surely her definition for parallel-ness would have been tripped up at some point over the past 3 years.
Megan and I had a bit of a conversation about her thinking but then I decided to throw it out to Twitter:
Having a modest Twitter following, I thought I might elicit responses from my usual cast of colleagues in the education world but I did not expect the amazing response that it got. Many were originally focused on explaining to me why she was wrong but that wasn't the question that I asked. What feedback would you give this child, aside from "right" and a pat on the head or "wrong" and send her back to her desk?
What came next was a rich mathematical conversation about parallel-ness of lines, what is a line and what is not a line, rules that we give students, and non-Euclidian geometry. The whole time, Megan and I watched my timeline and had great conversations about learning and mathematics.
Here are some of my favourite tweets, responses, challenges and debates:
What do we even mean when we say "line"? Do students make these distinctions?
We had great exchanges between educators, mathematicians and others who weighed in on the definitions we use and their limitations:
We had suggestions of expanding our mathematical vocabulary to include "curviparallel":
When we talk about parallel, are we limiting ourselves to 2-dimensions? What happens in 3-D?
We had debates about the correctness of her answer:
And there were great questions about the limitations of the definitions that we assume students know and understand:
I was curious to see what Professor Google had to say about the word parallel as I'm sure many parents and students would begin (and end) their search there. Here is what I found:
Oddly enough, both of these definitions contain the same misconception that my daughter had about two lines that never touch. I also had a look in the glossary of the Ontario Grades 1-8 Mathematics Curriculum and here is what I found:
Here are my current take-aways from this experience. I'm sure there will be more to follow as I have more time to process my thinking:
1. We need to be clear when using mathematical terminology. We need to be careful when reducing mathematics to a series of rules that need to be memorized and regurgitated as many of the rules that we teach expire as students move through their mathematics learning.
2. Assume nothing. My daughter is an excellent student and should be familiar with the concept of parallel-ness because she first learned it in grade 3 and has been working with it for three years. Assuming students have a complete understanding of mathematical terminology opens us to allowing misconceptions to go unnoticed. Getting students to talk about math and exploring incorrect answers is a really important part of learning.
3. Examine our own biases. I have a degree in mathematics, but my area of focus in my coursework was in advanced statistics. Admittedly my understanding of geometry, though not too bad, is not at the level of many who joined in the conversation about a grade 6 student's math worksheet. I had never really considered talking to her about hyperbolic geometry or circles with their centre at infinity but as a result of the learning that took place, we talked about these things!
4. Saving the best for last, we continued this conversation all weekend and will continue to do so in the future. I love to learn and I love to talk with children about mathematics, be it my own or my students. This experience has my mind buzzing about many things and I thank the almost 30000 people who had a look at an 11-year old's math homework and those who took the time to share their thinking!















Comments
Post a Comment